Active Probabilistic Inference on Matrices for Pre-Conditioning in Stochastic Optimization
2019
Conference Paper
ei
pn
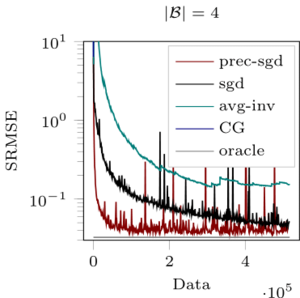
Pre-conditioning is a well-known concept that can significantly improve the convergence of optimization algorithms. For noise-free problems, where good pre-conditioners are not known a priori, iterative linear algebra methods offer one way to efficiently construct them. For the stochastic optimization problems that dominate contemporary machine learning, however, this approach is not readily available. We propose an iterative algorithm inspired by classic iterative linear solvers that uses a probabilistic model to actively infer a pre-conditioner in situations where Hessian-projections can only be constructed with strong Gaussian noise. The algorithm is empirically demonstrated to efficiently construct effective pre-conditioners for stochastic gradient descent and its variants. Experiments on problems of comparably low dimensionality show improved convergence. In very high-dimensional problems, such as those encountered in deep learning, the pre-conditioner effectively becomes an automatic learning-rate adaptation scheme, which we also empirically show to work well.
| Author(s): | de Roos, F. and Hennig, P. |
| Book Title: | Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics (AISTATS) |
| Volume: | 89 |
| Pages: | 1448--1457 |
| Year: | 2019 |
| Month: | April |
| Editors: | Kamalika Chaudhuri and Masashi Sugiyama |
| Publisher: | PMLR |
| Department(s): | Empirical Inference, Probabilistic Numerics |
| Bibtex Type: | Conference Paper (conference) |
| Paper Type: | Conference |
| Event Place: | Naha, Okinawa, Japan |
| State: | Published |
| URL: | https://arxiv.org/abs/1902.07557 |
| Links: |
PDF
|
|
BibTex @conference{deroos2019active,
title = {Active Probabilistic Inference on Matrices for Pre-Conditioning in Stochastic Optimization},
author = {de Roos, F. and Hennig, P.},
booktitle = {Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics (AISTATS)},
volume = {89},
pages = {1448--1457},
editors = {Kamalika Chaudhuri and Masashi Sugiyama},
publisher = {PMLR},
month = apr,
year = {2019},
doi = {},
url = {https://arxiv.org/abs/1902.07557},
month_numeric = {4}
}
|
|