Probabilistic Line Searches for Stochastic Optimization
2015
Conference Paper
ei
pn
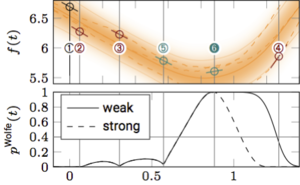
In deterministic optimization, line searches are a standard tool ensuring stability and efficiency. Where only stochastic gradients are available, no direct equivalent has so far been formulated, because uncertain gradients do not allow for a strict sequence of decisions collapsing the search space. We construct a probabilistic line search by combining the structure of existing deterministic methods with notions from Bayesian optimization. Our method retains a Gaussian process surrogate of the univariate optimization objective, and uses a probabilistic belief over the Wolfe conditions to monitor the descent. The algorithm has very low computational cost, and no user-controlled parameters. Experiments show that it effectively removes the need to define a learning rate for stochastic gradient descent. [You can find the matlab research code under `attachments' below. The zip-file contains a minimal working example. The docstring in probLineSearch.m contains additional information. A more polished implementation in C++ will be published here at a later point. For comments and questions about the code please write to mmahsereci@tue.mpg.de.]
| Author(s): | Mahsereci, M. and Hennig, P. |
| Book Title: | Advances in Neural Information Processing Systems 28 |
| Pages: | 181--189 |
| Year: | 2015 |
| Editors: | C. Cortes, N.D. Lawrence, D.D. Lee, M. Sugiyama and R. Garnett |
| Publisher: | Curran Associates, Inc. |
| Department(s): | Empirical Inference, Probabilistic Numerics |
| Research Project(s): | |
| Bibtex Type: | Conference Paper (inproceedings) |
| Event Name: | 29th Annual Conference on Neural Information Processing Systems (NIPS 2015) |
| Event Place: | Montreal, Canada |
| State: | Published |
| URL: | http://papers.nips.cc/paper/5753-probabilistic-line-searches-for-stochastic-optimization.pdf |
| Attachments: |
Matlab research code
|
|
BibTex @inproceedings{MahHen2015,
title = {Probabilistic Line Searches for Stochastic Optimization},
author = {Mahsereci, M. and Hennig, P.},
booktitle = {Advances in Neural Information Processing Systems 28},
pages = {181--189},
editors = {C. Cortes, N.D. Lawrence, D.D. Lee, M. Sugiyama and R. Garnett},
publisher = {Curran Associates, Inc.},
year = {2015},
doi = {},
url = {http://papers.nips.cc/paper/5753-probabilistic-line-searches-for-stochastic-optimization.pdf}
}
|
|