Artificial intelligent systems build models of their environment from observations, and choose actions that they predict will have beneficial effect on the environment's state. A central challenge is that the mathematical models used in this process call for computations that have no closed, analytic solution. Learning machines thus rely on a whole toolbox of numerical methods: High-dimensional integration routines are used for marginalization and conditioning in probabilistic models. Fitting of parameters poses nonlinear (and often non-convex) optimization problems. And the prediction of dynamic changes in the environment involves various forms of differential equations. In addition, there are special cases for each of these areas in which the computation amounts to large-scale linear algebra (i.e. Gaussian conditioning, least-squares optimization, linear differential equations). Traditionally, machine learning researchers have served these needs by taking numerical methods "off the shelf" and treating them as black boxes.
Since the 1970s, researchers like Wahba, Diaconis and O'Hagan repeatedly pointed out that, in fact, numerical methods can themselves be interpreted as statistical estimation methods -- as acting, learning machines: Numerical methods estimate an unknown, intractable, latent quantity given computable, tractable, observable quantities. For example, an integration method estimates the value of an integral given access to evaluations of the integrand. This is a rather abstract observation, but Diaconis and O'Hagan separately made a precise connection between inference and compuation in the case of integration: Several classic quadrature rules, e.g. the trapezoidal rule, can be interpreted as the maximum a posteriori (MAP) estimator arising from a certain family of Gaussian process priors on the integrand.
 Over recent years, the research group on probabilistic numerics has been able to add more such bridges between computation and inference, across the domains of numerical computation, by showing that various basic numerical methods are MAP estimates under equally basic probabilistic priors: quasi-Newton methods, such as the BFGS rule, arise as the mean of a Gaussian distribution over the elements of the inverse Hessian matrix of an optimization objective [ ]. This result can be extended to linear solvers [ ], in particular the method of conjugate gradients for linear problems (which amounts to Gaussian regression on the elements of the inverse of a symmetric matrix). And regarding ordinary differential equations, various Runge-Kutta methods can be interpreted as autoregressive filters [ ], returning a Gaussian process posterior over the solution of a differential equation.
Over recent years, the research group on probabilistic numerics has been able to add more such bridges between computation and inference, across the domains of numerical computation, by showing that various basic numerical methods are MAP estimates under equally basic probabilistic priors: quasi-Newton methods, such as the BFGS rule, arise as the mean of a Gaussian distribution over the elements of the inverse Hessian matrix of an optimization objective [ ]. This result can be extended to linear solvers [ ], in particular the method of conjugate gradients for linear problems (which amounts to Gaussian regression on the elements of the inverse of a symmetric matrix). And regarding ordinary differential equations, various Runge-Kutta methods can be interpreted as autoregressive filters [ ], returning a Gaussian process posterior over the solution of a differential equation.
The picture emerging from these connections is a mathematically precise description of computation itself as the active collection of information. In this view, the analytic description of a numerical task provides a prior probability measure over possible solutions; which can be shrunk towards the limit of a point measure through conditioning on the result of tractable computations. Many concepts and philosophical problems from statistics carry over to computation quite naturally, with two notable differences: First, in numerical ``inference'' tasks, the validity of the prior can be analysed to a higher formal degree than in inference from physical data sources, because the task is specified in a formal (programming) language. Secondly, since numerical routines are the bottom, ``mechanistic'' layer of artificial intelligence, the ``inner loop'', they are subject to strict requirements on computational complexity. Internally, a numerical method can only use tractable floating-point operations. This translates into a constraint on acceptable probabilistic models -- most basic numerical methods make Gaussian assumptions.
In the context of machine learning, the description of numerical computation as the collection of information has opened a number of research directions:
(1) Once it is clear that a numerical method uses an implicit prior, it is natural to adapt this prior to reflect available knowledge about the integrand. This design of "customized numerics" was used in a collaboration with colleagues at Oxford to build an efficient active integration method that outperforms Monte Carlo integration methods in wall-clock time on integration problems of moderate dimensionality [ ]. 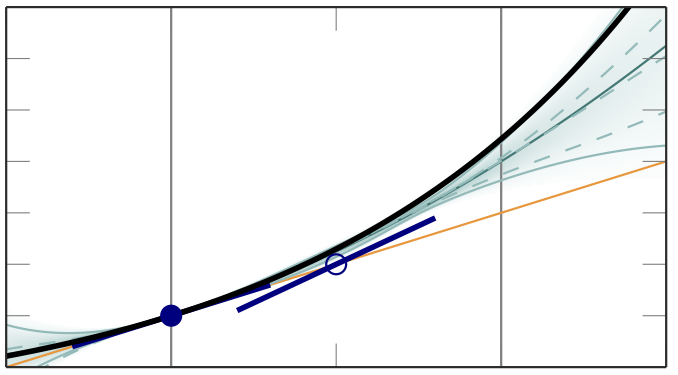
(2) Many numerical problems are defined relative to a setup that is itself uncertain to begin with. Once numerical methods are defined as probabilistic inference, such uncertainty can often be captured quite naturally. In a collaboration with colleagues in Copenhagen, it was shown [ ] how uncertainty arising from a medical imaging process can be propagated in an approximate inference fashion to more completely model uncertainty over neural pathways in the human brain.
(3) Explicit representations of uncertainty can also be used to increase robustness of a numerical computation itself. Addressing a pertinent issue in deep learning, we constructed a line search method [ ]---an elementary building block of nonlinear optimization methods---that is able to work with gradient evaluations corrupted by noise. This method drastically simplifies the problem of choosing a step size for the stochastic gradient descent methods used to train deep neural networks.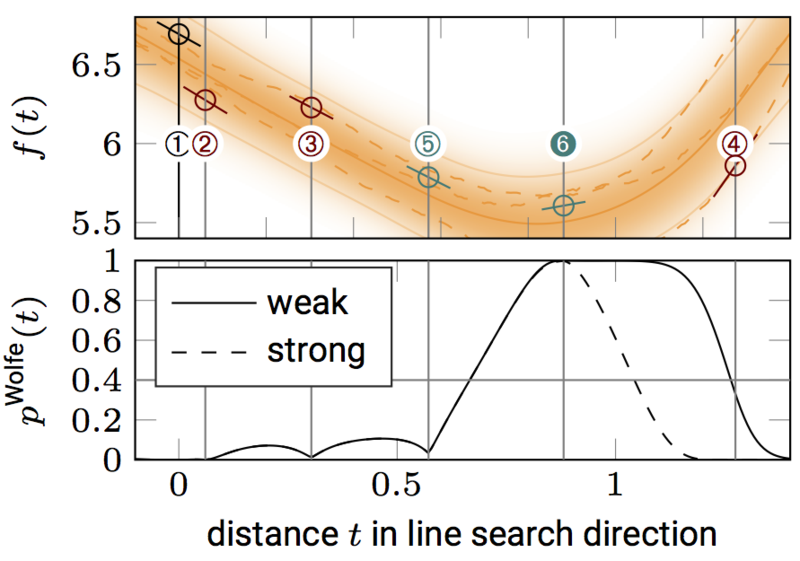
(4) More generally, it is possible to define probabilistic numerical methods: Algorithms that accept probability measures over a numerical problem as inputs, and return another probability measure over the solution of the problem, which reflects both the effect of the input uncertainty, and uncertainty arising from the finite precision of the internal computation itself. A position paper [ ] motivates this class of methods and suggests their use for the control of computational effort across heterogeneous, composite chains of computations, such as those that make up intelligent machines. In collaboration with the Optimization group at the German Cancer Research Centre we developed an approximate inference framework to propagate physical uncertainties through the planning (optimization) pipeline for radiation treatment, to lower the risk of unnecessary complications for cancer patients [ ].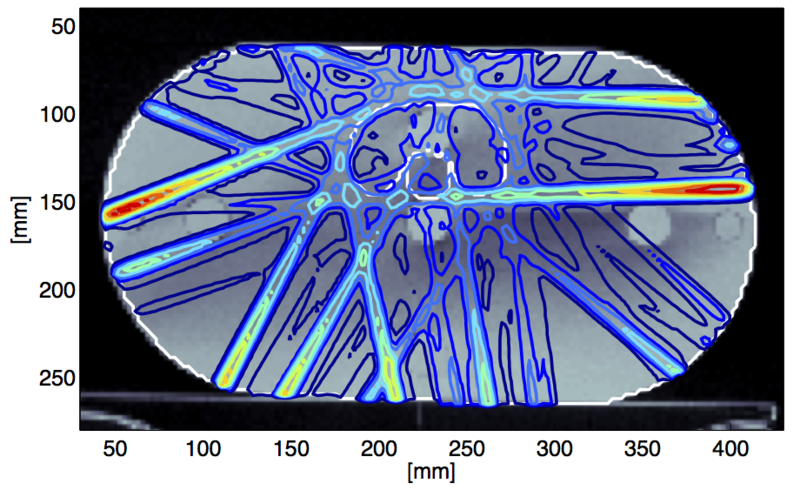
In a separate but related development, a community has also arisen around the formulation of global optimization as inference, and the formulation of sample-efficient optimization methods. These Bayesian Optimization methods can, for example, be used to structurally optimize, automate the design of machine learning models themselves. We contributed to this area with the development of the Entropy Search [ ] algorithm that automatically performs experiments expected to provide maximal information about the location of a function's extremum.
The study of probabilistic numerical methods is emerging as a new field at the intersection of mathematics, computer science and statistics. As co-founders of this area, the research group on probabilistic numerics plays a central role in its development. The Intelligent Systems community, with their intractably large data streams and non-analytic model classes, are simultaneously contributors and beneficiaries of this development. Equipping computational routines with a meaningful notion of uncertainty stands to increase both the efficiency and reliability of intelligent systems at large.
